Используя рисунок, определите верное утверждение и укажите его номер.
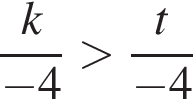


Используя рисунок, определите верное утверждение и укажите его номер.
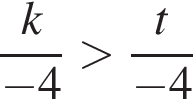


Величины a и b являются прямо пропорциональными. Используя данные таблицы, найдите неизвестное значение величины a.
| a | 2,9 | |
| b | 114 | 8,7 |
Дан треугольник ABC, в котором AC = 21. Используя данные рисунка, найдите длину стороны AB треугольника ABC.
Две окружности с центрами A и B касаются в точке M. Найдите длину отрезка CN, если
 и диаметр большей окружности на 35 больше радиуса меньшей окружности.
и диаметр большей окружности на 35 больше радиуса меньшей окружности.
Найдите значение выражения 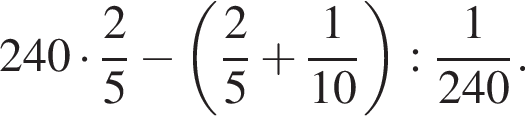
Найдите наименьший положительный корень уравнения 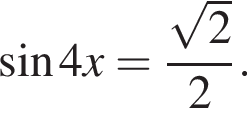
Сумма всех натуральных решений неравенства 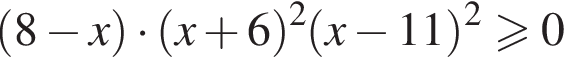 равна:
равна:
Укажите уравнение, равносильное уравнению 
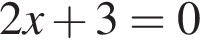
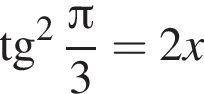
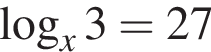
Среди чисел ![]()
![]()
![]()
![]()
![]() укажите то, которое является решением системы неравенств
укажите то, которое является решением системы неравенств 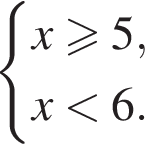
Укажите номер квадратного уравнения, корнями которого являются числа x1 − 1, x2 − 1, где x1, x2 — корни квадратного уравнения 2x2 − 7x − 3 = 0.
1) x2 + x − 3 = 0;
2) 2x2 + 11x + 10 = 0;
3) 2x2 − 3x − 8 = 0;
4) 2x2 + 3x − 8 = 0;
5) 2x2 − 11x + 10 = 0.
Строительные бригады №1 и №2 купили соответственно 18 и 19 фундаментных блоков у одного из трех поставщиков, выбрав для себя наиболее дешевый вариант. Стоимость одного блока и условия доставки всей покупки приведены в таблице. Определите, на сколько рублей дороже обошлась эта покупка с доставкой одной из бригад. Ответ запишите в рублях.
| Поставщик | Стоимость (тыс. руб. за 1 шт.) | Стоимость доставки (тыс. руб. за всю покупку) | Специальное предложение |
|---|---|---|---|
| 1 | 205 | 1850 | — |
| 2 | 240 | 1950 | Доставка со скидкой 50 %, если сумма заказа превышает 4,5 млн. бел. рублей |
| 3 | 275 | 2050 | Доставка бесплатно, если сумма заказа превышает 5 млн. бел. рублей |
Найдите произведение большего корня на количество корней уравнения 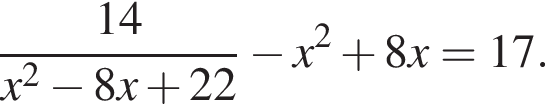
Результат упрощения выражения 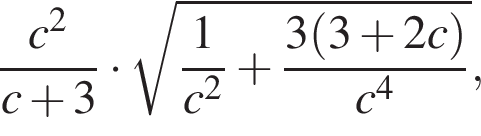 если
если 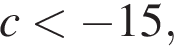 равен ... .
равен ... .
Площадь прямоугольника ABCD равна 50. Точки M, N, P, Q — середины его сторон. Найдите площадь четырехугольника между прямыми AN, BP, CQ, DM.
Найдите периметр правильного шестиугольника, меньшая диагональ которого равна ![]()
На круговой диаграмме представлена информация о продаже 200 кг овощей в течение дня. Для начала каждого из предложений А — В подберите его окончание 1 — 6 так, чтобы получилось верное утверждение.
А) Масса (в килограммах) проданной капусты равна ...
Б) Отношение, выраженное в процентах, которое показывает, на сколько масса проданного картофеля меньше массы проданных помидоров, равно ...
В) Отношение, выраженное в процентах, которое показывает, на сколько масса проданной свеклы больше массы проданного лука, равно ...
1) 25
2) 40
3) 4
4) 125
5) 38
6) 19
Ответ запишите в виде сочетания букв и цифр, соблюдая алфавитную последовательность букв левого столбца. Помните, что некоторые данные правого столбца могут использоваться несколько раз или не использоваться вообще. Например: А1Б1В4.
Выберите три верных утверждения:
1) если 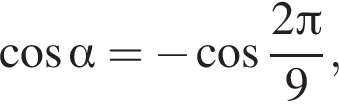 то
то 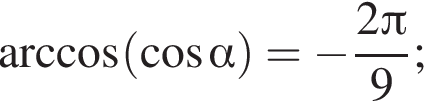
2) если 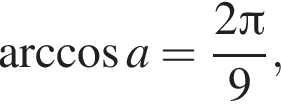 то
то 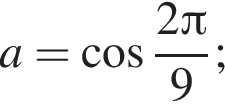
3) если 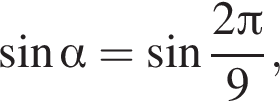 то
то 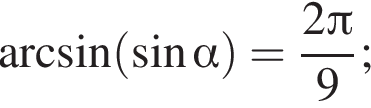
4) если 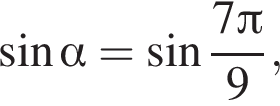 то
то 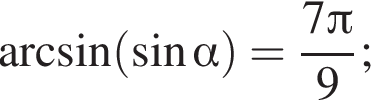
5) если 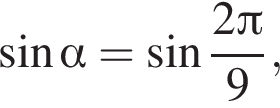 то
то 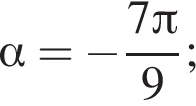
6) если 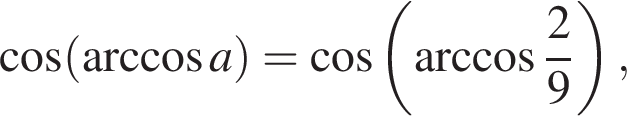 то
то 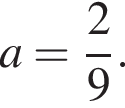
Ответ запишите цифрами (порядок записи цифр не имеет значения). Например: 123.
На координатной плоскости даны точки A(1; −3) и D(−5; −3). Точка С симметрична точке А относительно оси абсцисс, а точка В симметрична точке D относительно начала координат. Для начала каждого из предложений А−В подберите его окончание 1−6 так, чтобы получилось верное утверждение.
| Начало предложения | Окончание предложения |
|---|---|
A) Длина большей диагонали четырехугольника ABCD равна ... Б) Длина наибольшей стороны четырехугольника ABCD равна ... B) Площадь четырехугольника ABCD равна ... | 1) 2) 36 3) 30 4) 5) 24 6) |
Ответ запишите в виде сочетания букв и цифр, соблюдая алфавитную последовательность букв левого столбца. Помните, что некоторые данные правого столбца могут использоваться несколько раз или не использоваться вообще. Например: А1Б1В4.
Найдите сумму целых решений неравенства 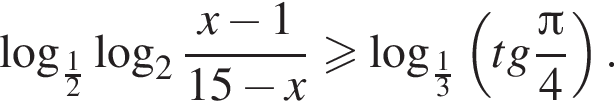
В равнобедренную трапецию, площадь которой равна 115, вписана окружность радиуса 5. Найдите периметр трапеции.
Найдите значение выражения 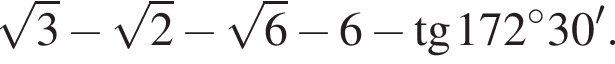
Числовая последовательность (an) задана формулой n-го члена 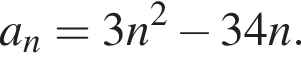 Найдите наименьший член am этой последовательности и его номер m. В ответ запишите значение выражения m · am.
Найдите наименьший член am этой последовательности и его номер m. В ответ запишите значение выражения m · am.
Пусть 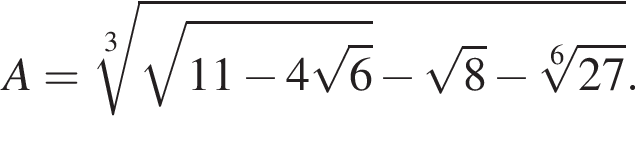 Найдите значение выражения A12.
Найдите значение выражения A12.
Найдите площадь полной поверхности прямой треугольной призмы, описанной около шара, если площадь основания призмы равна 11,5.
Верхнюю сторону листа фанеры прямоугольной формы разделили для покраски прямой линией на две части так, как показано на рисунке. Треугольную часть (I) покрасили краской белого цвета, а четырехугольную (II) — краской серого цвета. Сколько серой краски (в граммах) было использовано, если краски белого цвета понадобилось 270 г и расход краски (г/см2) обоих цветов одинаков?
Найдите произведение точек минимума функции 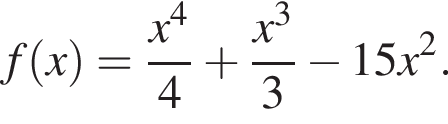
Найдите сумму всех целых чисел из области определения функции 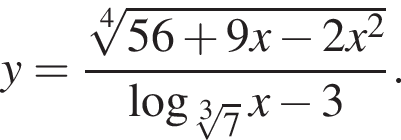
Найдите произведение корней уравнения 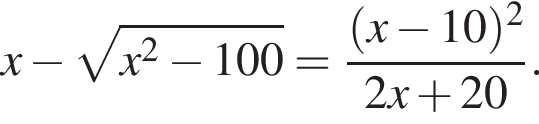
Найдите все пары (m, n) целых чисел, которые связаны соотношением m2 + 2m = n2 + 6n + 13. Пусть k — количество таких пар, m0 — наименьшее из значений m, тогда значение выражения k · m0 равно ... .
На стороне BC прямоугольника ABCD отмечена точка O так, что 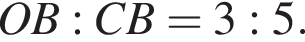 Из точки O восстановлен перпендикуляр SO к плоскости прямоугольника. Найдите объем пирамиды ABCDS, если известно, что
Из точки O восстановлен перпендикуляр SO к плоскости прямоугольника. Найдите объем пирамиды ABCDS, если известно, что 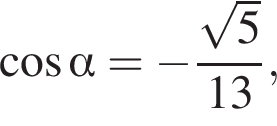 где
где ![]() — линейный угол двугранного угла BSAD,
— линейный угол двугранного угла BSAD, 
